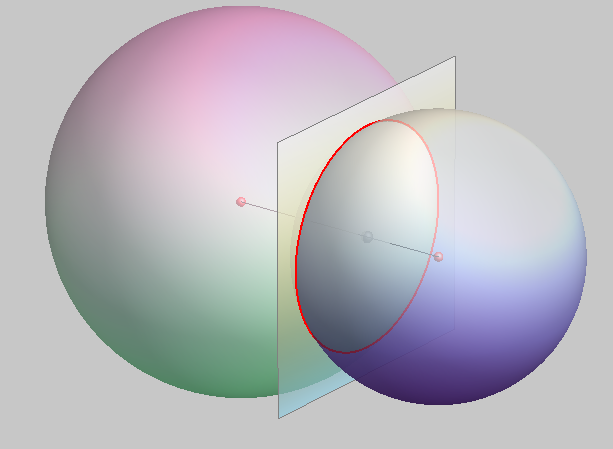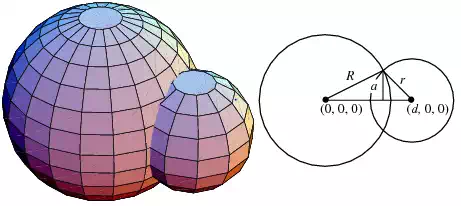
Let two spheres of radii ![]() and
and ![]() be located along the x-axis centered at
be located along the x-axis centered at ![]() and
and ![]() , respectively. Not surprisingly, the analysis is very similar to the case of the circle-circle intersection. The equations of the two spheres are
, respectively. Not surprisingly, the analysis is very similar to the case of the circle-circle intersection. The equations of the two spheres are
| (1) | |||
| (2) |
Combining (1) and (2) gives
| (3) |
Multiplying through and rearranging give
| (4) |
Solving for ![]() gives
gives
| (5) |
The intersection of the spheres is therefore a curve lying in a plane parallel to the ![]() -plane at a single
-plane at a single ![]() -coordinate. Plugging this back into (◇) gives
-coordinate. Plugging this back into (◇) gives
| (6) | |||
| (7) |
which is a circle with radius
| (8) | |||
| (9) |
The volume of the three-dimensional lens common to the two spheres can be found by adding the two spherical caps. The distances from the spheres’centers to the bases of the caps are
| (10) | |||
| (11) |
so the heights of the caps are
| (12) | |||
| (13) |
The volume of a spherical cap of height ![]() for a sphere of radius
for a sphere of radius ![]() is
is
| (14) |
Letting ![]() and
and ![]() and summing the two caps gives
and summing the two caps gives
| (15) | |||
| (16) |
This expression gives ![]() for
for ![]() as it must. In the special case
as it must. In the special case ![]() , the volume simplifies to
, the volume simplifies to
| (17) |
In order for the overlap of two equal spheres to equal half the volume of each individual sphere, the spheres must be separated by a distance
| (18) | |||
| (19) | |||
Sphere to Plane Contact Force (3D)
his block implements a contact force between a sphere and a plane. The force is active above and below the plane. This is part of the Simscape Multibody Contact Forces Library
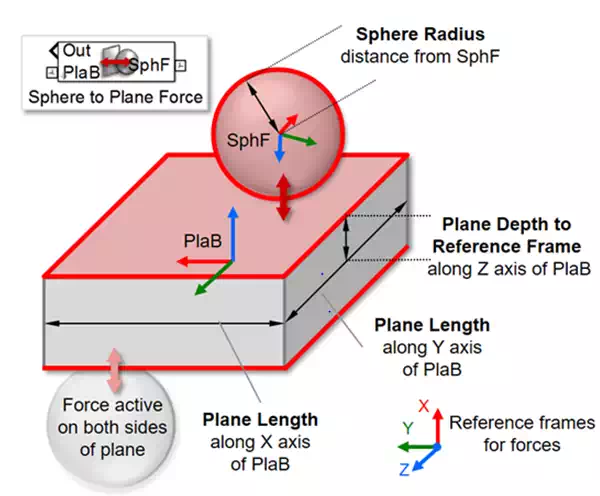
Frame connected to PlaB port:
- Located at midpoint of plane (x, y, and z).
- Z-axis is normal to the surfaces where force is active.
Frame connected to the SphF port:
- Located at center of sphere.
- Orientation does not matter.
Output signal is a bus with intermediate calculations and total force.