Spherical Capacitors
Consider an isolated, initially uncharged, metal conductor. After the first small amount of charge, q, is placed on the conductor, its voltage becomes  The capacitance of the spherical conductor can be calculated as The capacitance of the spherical conductor can be calculated as 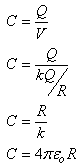 Notice that a spherical conductor’s capacitance is totally dependent on the sphere’s radius. Notice that a spherical conductor’s capacitance is totally dependent on the sphere’s radius. |
Parallel Plate Capacitors 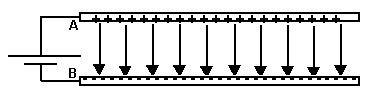 Since we know that the basic relationship Q = CV, we must obtain expressions for Q and V to evaluate C. Using Gauss’ Law, Since we know that the basic relationship Q = CV, we must obtain expressions for Q and V to evaluate C. Using Gauss’ Law, 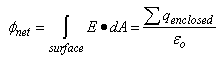 We can evaluate E, the electric field between the plates, once we employ an appropriate gaussian surface. In this case, we will use a box with one side embedded within the top plate. We can evaluate E, the electric field between the plates, once we employ an appropriate gaussian surface. In this case, we will use a box with one side embedded within the top plate. 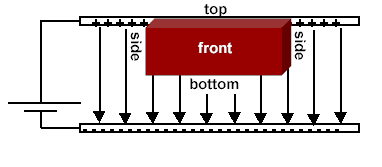 This box has six faces: a top, a bottom, left side, right side, front surface and back surface. Since the top surface is embedded within the metal plate, no field lines will pass through it since under electrostatic conditions there are no field lines within a conductor. Field lines will only run parallel to the area vector of the bottom surface. They will be perpendicular to the area vectors of the other four sides. Thus, This box has six faces: a top, a bottom, left side, right side, front surface and back surface. Since the top surface is embedded within the metal plate, no field lines will pass through it since under electrostatic conditions there are no field lines within a conductor. Field lines will only run parallel to the area vector of the bottom surface. They will be perpendicular to the area vectors of the other four sides. Thus, 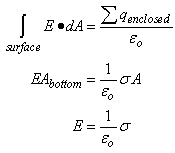 We also know that the potential difference across the plates is equal to We also know that the potential difference across the plates is equal to 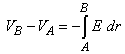 Since plate B is defined to be at V = 0, Since plate B is defined to be at V = 0,  we can rewrite this as we can rewrite this as 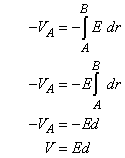 Substituting into Q = CV yields Substituting into Q = CV yields 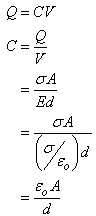 To relate the energy per unit volume stored in a capacitor to the magnitude of its electric field, we will build on our relationship for the energy stored in a capacitor developed in a previous lesson. To relate the energy per unit volume stored in a capacitor to the magnitude of its electric field, we will build on our relationship for the energy stored in a capacitor developed in a previous lesson. 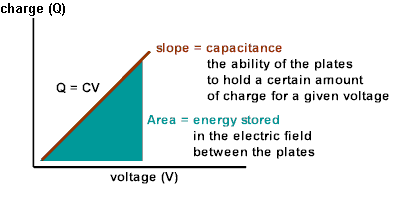  Cylindrical Capacitors Now let’s consider the geometry of a cylindrical capacitor. Suppose that our capacitor is composed of an inner cylinder with radius a enclosed by an outer cylinder with radius b. Cylindrical Capacitors Now let’s consider the geometry of a cylindrical capacitor. Suppose that our capacitor is composed of an inner cylinder with radius a enclosed by an outer cylinder with radius b. 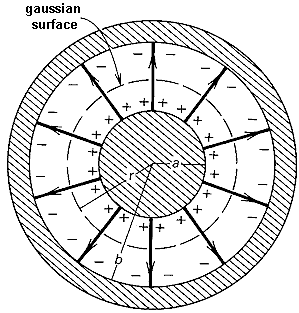 Since we know that the basic relationship Q = CV, we must obtain expressions for Q and V to evaluate C. Again, we will use Gauss’ Law to evaluate the electric field between the plates by using a gaussian surface that is cylindrical in shape and of length L. The cylinder has a uniform charge per unit length of Since we know that the basic relationship Q = CV, we must obtain expressions for Q and V to evaluate C. Again, we will use Gauss’ Law to evaluate the electric field between the plates by using a gaussian surface that is cylindrical in shape and of length L. The cylinder has a uniform charge per unit length of  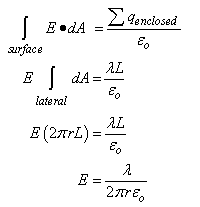 We also know that the potential difference across the cylinders is equal to We also know that the potential difference across the cylinders is equal to 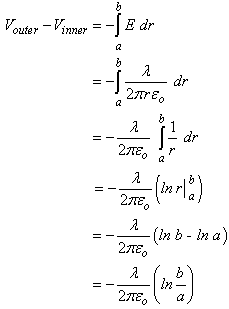 Since the outer plate is negative, its voltage can be set equal to 0, and we can state that the potential difference across the capacitors equals Since the outer plate is negative, its voltage can be set equal to 0, and we can state that the potential difference across the capacitors equals 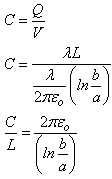 This represents the capacitance per unit length of our cylindrical capacitor. An excellent example of a cylindrical capacitor is the coaxial cable used in cable TV systems. |