we will review two solutions methods, Gauss iteration with a variant called Gauss-Seidel iterative method, and the NewtonRaphson method.
Solution by Gauss-Seidel Iteration





Newton-Raphson Method
Before applying this method to the power flow problem we review the iteration scheme and some of its properties. A system of nonlinear algebraic equations can be written as f(x) = 0 (6.12) where x is an n-vector of unknowns and f is an n-vector function of x. Given an appropriate starting value x 0 , the Newton-Raphson method solves this
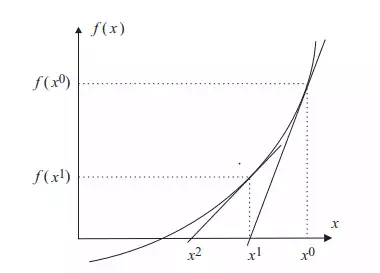
Newton-Raphson method in one-dimensional case
One-dimensional case

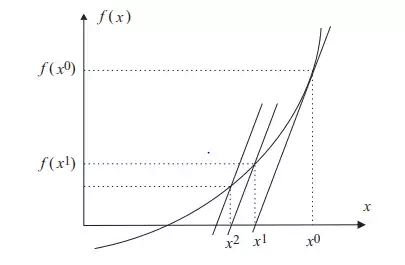
Dishonest Newton-Raphson method in one-dimensional case

Quadratic Convergence
Close to the solution point x ∗ , the Newton-Raphson method normally presents a property called quadratic convergence. This can be proved for the unidimensional case discussed above if it is assumed that x ∗ is a simple (not a multiple) root and that its first and second derivatives are continuous.

Multidimensional Case





